The formulas stated above assume the corners to be a perfect arc of a circle. In practice, the shape of the corner is between an arc and a chamfer. Therefore, the calculated diagonal should be considered as a nominal value as the actual diagonal will be smaller than the calculated value.
Note that when all three variables are specified, S, D and R must be in relation to each other. When only the size and diagonal are specified, the resulting corner radius must be determined. The practical minimum radius is .002″, which results in a sharp-cornered square wire. As tolerances must be accommodated, it is advisable to calculate S and D maximum and minimum, to get the complete envelope. Minimum and maximum R can then be determined.
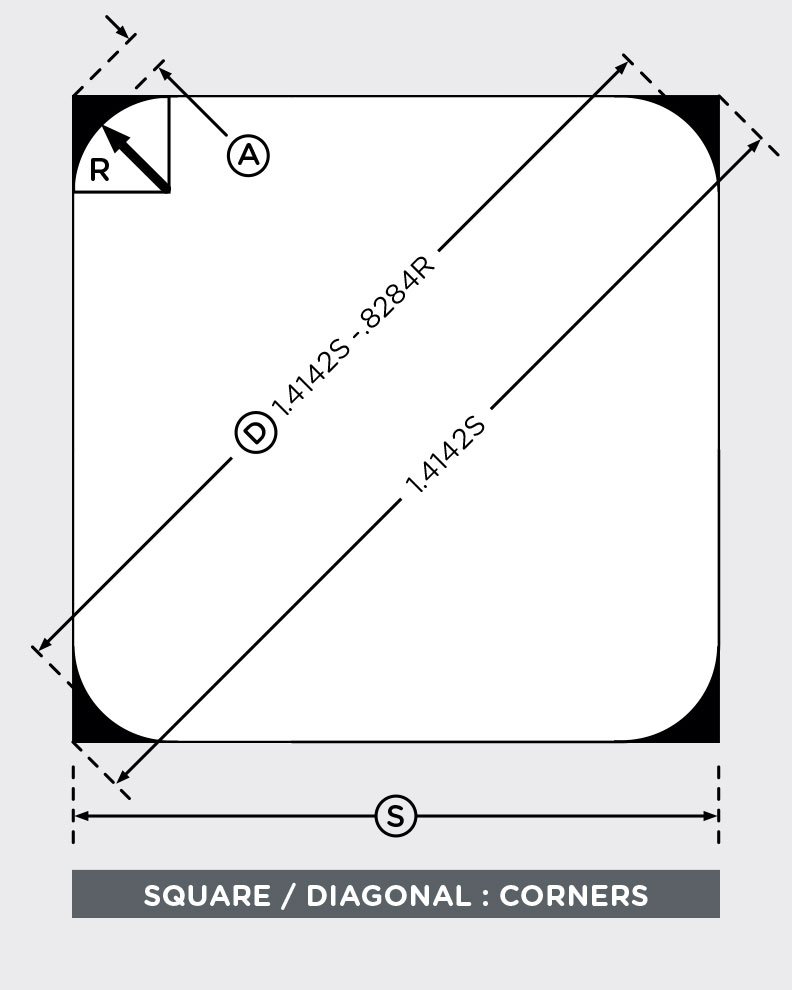
The relationship between a square and its diagonal is straightforward:
D = Diagonal | S = Square Area
D = √2S
D = 1.4142 S
The allowance for corner radii is more complex:
A = Allowance per Corner | R = Corner Radius
A = √2R – R
A = R (√2-1)
Since there are two corners involved in every diagonal, the total allowance is 2A per diagonal.
Putting all this together into one equation it becomes:
D = 1.4142 S – .8284 R
Or when D and R are known:
S = D + .8284 R / 1.4142
Or when D and S are known:
R = 1.4142 S – D / .8284
The formulas stated above assume the corners to be a perfect arc of a circle. In practice, the shape of the corner is between an arc and a chamfer. Therefore, the calculated diagonal should be considered as a nominal value as the actual diagonal will be smaller than the calculated value.
Note that when all three variables are specified, S, D and R must be in relation to each other. When only the size and diagonal are specified, the resulting corner radius must be determined. The practical minimum radius is .002″, which results in a sharp-cornered square wire. As tolerances must be accommodated, it is advisable to calculate S and D maximum and minimum, to get the complete envelope. Minimum and maximum R can then be determined.
The relationship between a square and its diagonal is straightforward:
D = Diagonal | S = Square Area
D = √2S
D = 1.4142 S
The allowance for corner radii is more complex:
A = Allowance per Corner | R = Corner Radius
A = √2R – R
A = R (√2-1)
Since there are two corners involved in every diagonal, the total allowance is 2A per diagonal.
Putting all this together into one equation it becomes:
D = 1.4142 S – .8284 R
Or when D and R are known:
S = D + .8284 R / 1.4142
Or when D and S are known: